「2019-1」【每周分享】什么是机器人比赛中的PID控制?
132545
0
22
2019-01-30
生活中我们经常会使用到恒温电器。比如空调、冰箱和电磁炉,这些电器都能够将自己的工作环境稳定在某一个温度。我们设置空调为16 °C,它就能将温度准确地降到 16 °C 而不是 15 °C;设置电磁炉 200°C,它也不会烧到 250°C。
这背后是一双无形的手在“控制”它们——PID 控制器。
控制,简单说,就是让一个东西听话。控制机器或是机器人,可以通过代码来实现,也可以通过电路来实现,这个控制逻辑可抽象地认为是一种控制算法。
PID (Proportion Integration Differentiation)是当前一种最主流的控制算法,优点在于简单高效,很多高级的控制算法也是在 PID 的基础上进行优化和演变的。
PID 的实现简单,应用广泛。在上述例子中,以空调为例,已知当前环境温度和用户设定温度, PID 控制器可以通过计算,来调节功率,使空调尽快到达用户设定的温度,并且保持稳定。
拓展阅读:PID 控制算法本质是个数学公式,有乘除有积分有微分,可以通过写代码或是电子元器件把这个数学公式表达出来,也就是有软硬件两种实现方式。随着计算机时代的发展,通过软件实现的数字式 PID 控制器成为主流。推荐书籍《自动控制原理》,邹见效,机械工业出版社。
◆◆◆
RoboMaster 比赛中的 PID 控制算法侧重于软件实现。在赛场上,PID 也同样的被应用在很多场景下的机器人状态控制。
比方说触发大能量机关,机器人要先识别屏幕上的指定数字,还要用 PID 来控制云台和发射机构(俗称枪口)快速和准确地射击数字。

大能量机关屏幕
上期我们已经教过,机器人如何通过机器学习,去识别出随机(随机位置+随机字体)的数字图像。识别完成后,机器人可以获得目标数字图像的位置,实际上等于获得了发射机构的目标角度。
上期回顾:《机器人如何在复杂的环境下进行视觉识别?》
下一步,怎么让枪口指向正确的角度,完成“突突”的射击呢?核心技术就是云台控制。
拓展阅读:在 RoboMaster 参赛机器人中,云台和发射机构是相连的,控制云台实际上就能够控制发射机构的瞄准角度。本文中我们讲解使用 PID 控制云台,当入门掌握之后,学习其他条件下的控制也是类似的道理。
我们先来了解一下什么是云台。云台是一种可以多角度摆动的物体,比如单反相机的三脚架上面,就会配备一个云台,可以摆出水平、倾斜或俯仰等角度。

三脚架上的云台
在 RoboMaster 比赛中,为了让机器人的枪口可以在一定角度内自由调整,同时为了保证在不平坦的场地运行时,发射机构能尽量稳定(减少枪口晃动),就会在机器人的底盘上加装一套云台。

机器人上的云台系统
赛场上的云台大多数是由无刷电机驱动的。通过改变电机的电流大小,可以调整电机运行的速度;通过改变电机的电流正负,可以调整电机的转动方向。
同时,电机内部还有传感器在记录电机的转动位置,再加上一定的算法处理,就可以知道云台应该摆在哪个方向,也就是实际角度值。
◆◆◆
知道了实际角度,机器人身上的控制器(主控)再发送电流值给云台电机,云台就可以完美地摆到目标角度吗?Too young, too native!
如果给云台电机发送很大的电流值,云台就可以快速往指定的方向运行,但这样很容易刹不住车,超过预期的目标位置;如果发送的电流太小,又会导致云台行动慢吞吞,跟不上大能量机关的数字刷新。因此,还要平衡云台的速度和精确度。
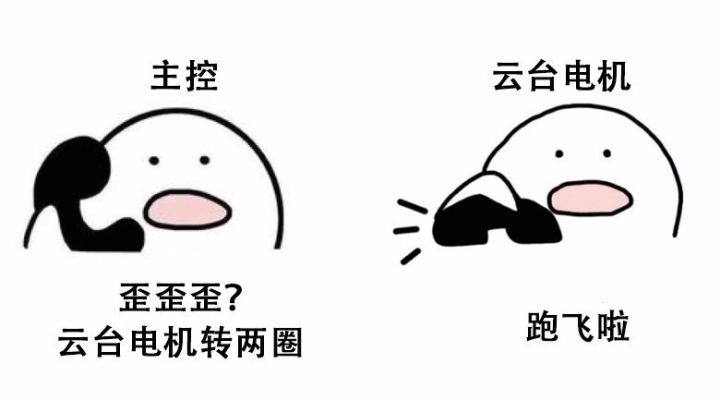
有效的办法就是,根据距离目标值的远近来调节云台的速度,离得远就转快一些,离得近就慢一些。这样就需要我们实时获取云台当前的实际角度,然后和目标角度做对比,根据差值来动态地调整云台的速度和方向。

机器人身上有很多电机
只根据上述的参数来调节还不足以达到云台控制的理想性能,为了让云台实现快速响应、减小误差、消除扰动,在实际控制过程中我们还要使用 PID 控制器。
PID 控制器
PID 控制器(比例-积分-微分控制器)是一种通过控制系统的偏差来调整输入信号的线性反馈控制算法。通俗的说,它可以给出使执行器(电机)快速准确到达目标的“指导方案”。
想要学 PID,让机器人能控制住寄几,首先要认识几个概念。
系统
系统是具有特定功能的整体,由相互作用、相互依赖的若干组成部分结合而成。
举个栗子:步兵机器人就是一个系统,镜头、小电脑、电机等等是相互作用和相互依赖的组成部分,共同完成了击打能量机关的任务。
反馈
反馈是指将系统输出量通过恰当的检测装置,返回到输入端,与输入量进行比较,并以某种方式改变输入,进而影响系统功能的过程。
举个栗子:我们想让机器人抬头 90°,结果它偷懒只抬了 60°,检测装置发现后,命令它再抬 30°,最后达到我们想要的 90°。
开环和闭环
一般管具有反馈环节的系统称为闭环控制系统,而没有反馈环节的系统则称为开环控制系统。
举个栗子:以步兵的云台控制系统为例。
开环控制系统:假设云台电机是个闭上眼的人,需要走到指定地点,但是因为他看不到,只有主控能告诉它怎么走。但是,主控也不知道还需要走多少步。
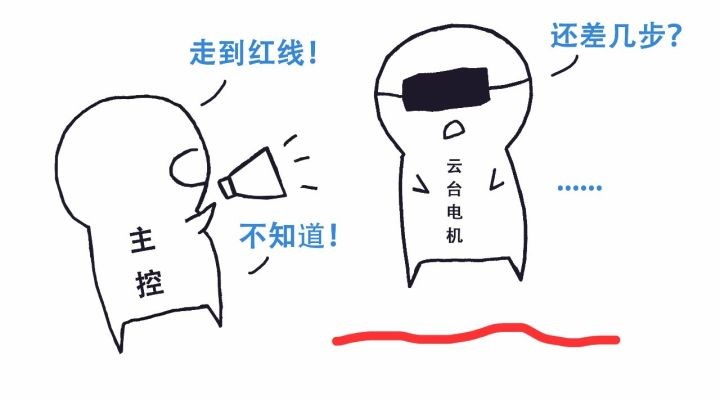
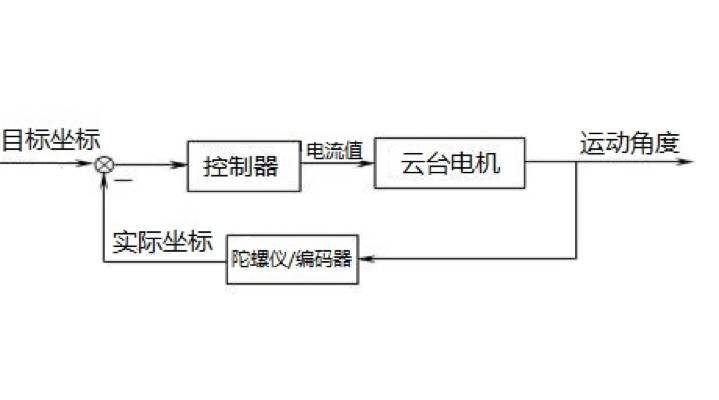
控制器(主控)获知目标坐标后,给云台电机一个电流值,云台电机就转一转,然后主控也不知道刚刚转了多少圈,就开始凭感觉给电流值,能不能达到目标坐标,随缘吧。
闭环控制系统:主控获得云台电机的实时位置和目标位置后,告诉云台电机应该怎么走。
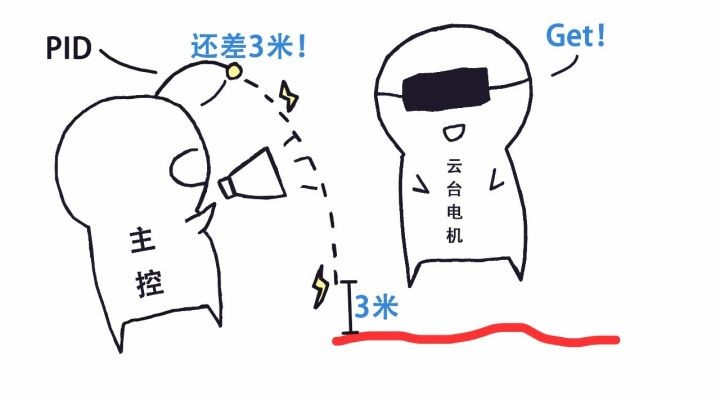
云台的实际坐标被陀螺仪/编码器(检测装置)记录下来实时发送给控制器(主控),控制器获知目标坐标后,通过计算得出目标电流值发送给云台电机,云台电机就运动一定角度。电机运动云台实际坐标会改变,主控就知道接下来还差多少角度,再计算发送电流值,如此循环。
传递函数
传递函数用于描述系统的输入与输出之间的关系。将系统的输入信号表示为函数 R(s),输出信号为函数 C(s),那么我们的系统闭环传递函数可以写成 G(S)=C(s)/(R(s))。
(看不懂没关系,小R也没看懂,不影响不影响。)
PID 的组成
PID 实际上是一个作用于闭环系统的控制算法,由三个部分组成,分别是 P 比例环节,I 积分环节,D 微分环节。
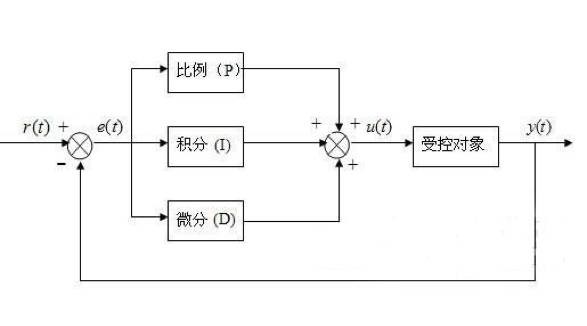
含有PID的闭环控制系统框图
我们通过三则卖萝卜的机器人故事,了解一下每个环节是做什么的。
P 比例环节
有一个机器人,就叫它一号吧,开了一家萝卜专卖店。它的工作是不断将新鲜萝卜从保鲜仓库摆放到货柜上供大家购买。如果拿太多萝卜出来,却没有顾客购买,一直放着会不新鲜,当然摆放萝卜数量也不能太少,否则许多顾客啥都没买到,专卖店也要倒闭了。
于是一号就观察萝卜的销售情况,每次补货时,如果萝卜卖得多就摆放多一点到货柜,卖得少时就放少一点到货柜。(这其实就是一个比例环节,比例环节的传递函数是 Gp (s)=Kp)
I 积分环节
经过一号的勤劳经营,店里的生意进入平稳发展期,来店购买萝卜的顾客都成了老熟客。节约的一号每次补货都尽可能恰好使每位顾客都能买到萝卜,但每次总有几个顾客不能及时买到萝卜需要等待补货。一号心想这样下去,老熟客都要气跑了。
于是一号动手做了一个新的机器人——二号。二号贴心地把每次补货前等待的顾客想要购买的萝卜数量都记在了小本本上,补货的时候都掏出小本本看一眼。(二号相当于一个积分环节,对每次的误差都进行累计积分,积分环节的传递函数是 Gi (s)=Ki/s)这样在一号和二号的合作下,老熟客们都心满意足买到了萝卜。
D 微分环节
一号的生意蒸蒸日上,它决定到一个新的城市开一家分店。新店初开,萝卜的售卖数量波动很大,要么眼看着萝卜热卖,补了许多萝卜,结果却无人问津白白浪费;要么想着萝卜卖得那么少,补货少一点,结果许多顾客蜂拥而入却空手而归。
绝望的一号又动手制作了新的机器人——三号。三号不只看这次补货前萝卜售卖情况,还会看上次补货前萝卜售卖情况,然后根据两次售卖情况的差值(也就是变化率)来预测接下来的售卖情况并补货(三号相当于一个微分环节,微分可以获得原值的变化率,比如说对路程进行微分可以得到速度。微分环节的传递函数是微分环节的传递函数是 Gd (s)=Kd*s)。有了三号的帮忙,分店的运营也逐渐走上了正轨。
在一二三号的合作下,不管萝卜销售情况如何,萝卜专卖店都能提供合适数量的萝卜供顾客购买又不致造成浪费,这也是 PID 控制的美妙之处。(PID 的传递函数我们将上文提到的三个环节的传递函数并联相加可以写成 G(s)=Kp+Ki/s+Kd*s)
PID 代码理解
接下来,我们用伪代码描述一下 PID 三个环节的工作:
古娜拉黑暗之神!无限循环!
{
本次误差 = 目标值-实际值
P输出 =Kp *本次误差
I输出 += Ki*本次误差
D输出 =Kd *(本次误差-上次误差)/*由于软件实现是个离散的,故用差分代替微分*/
PID输出 = P输出+I输出+D输出
上次误差 = 本次误差 /*每次循环结束前记得更新上次误差值哟~*/
}
(好的,谢谢伪代码君)
PID 运用实战
MATLAB 中的 Simulink 组件可以用来仿真含有 PID 的系统,我们通过一次仿真实战一下。
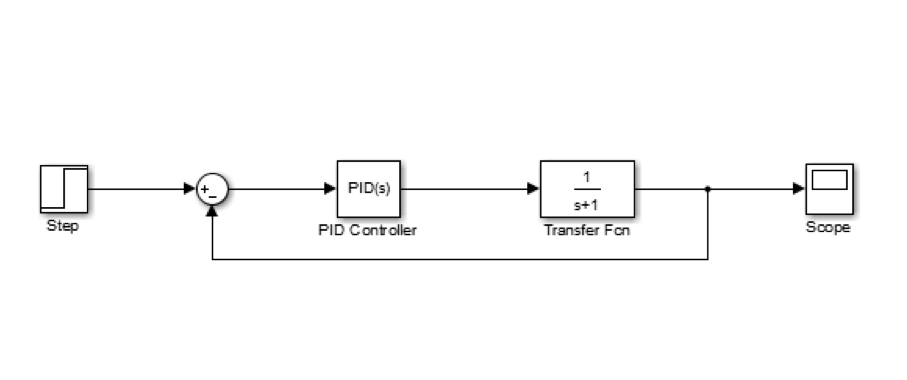
一个输入信号为阶跃信号
含有 PID 控制器的闭环系统
在 PID 控制器中仅改变 Kp 的值,Kd、Ki 保持为 0,通过示波器波形我们可以发现:
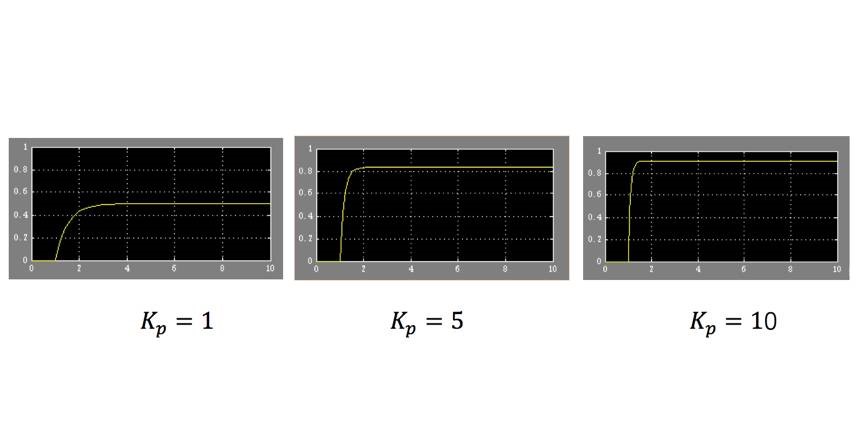
通过调节 Kp 我们可以改变系统的响应速度及系统的稳态误差,随着 Kp 的增大,系统相应速度加快,静态误差也逐渐减小。听起来似乎 Kp 是越大越好,其实不然,Kp 的增大时系统的截止频率随之增大,但相频特性不受 Kp 影响,因此系统的相位裕度也会随之减小,系统稳定性减弱。
由于仅仅有比例环节无法消除系统静态误差,我们给系统加入积分环节。保持 Kp=10,Kd=0,改变 Ki 的值。

通过示波器波形我们可以看到 Ki 过小时消除稳态误差所需时间较长,而 Ki 过大时则会引起系统振荡。积分环节可以提高系统类型,消除稳态误差,但同时积分环节引入了-90°相位,降低了系统的稳定性,Ki 调节不当时甚至会造成系统不稳定。
最后我们加上微分环节,保持 Kp=10,Ki=10,改变 Kd 的值。
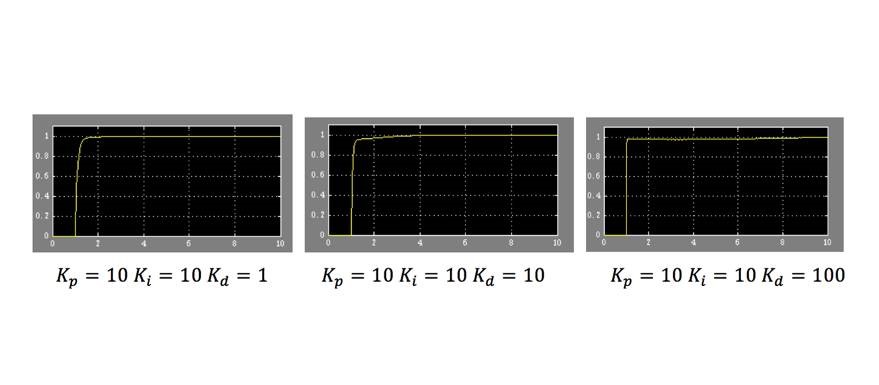
由示波器波形我们可以看出提高 Kd 加快系统的动态响应,但是 Kd 过大时在系统进入稳态后会放大噪声,减小系统的抗干扰能力。
实战结束,我们再来回顾一下 PID 各个环节对系统的控制作用。
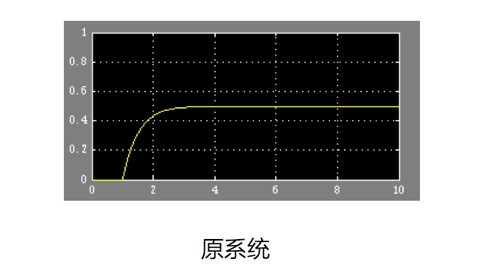
我们可以看到原系统中曲线趋于平衡的时间是 3s 之后,而且稳定时纵坐标距离目标值1还有半截距离。

加入 P 环节之后,曲线 2s 前就趋于平衡,时间缩短了, 同时稳定时纵坐标距离目标值1的距离缩短了,但始终还是存在一段距离是无法通过增大系数来消除的。
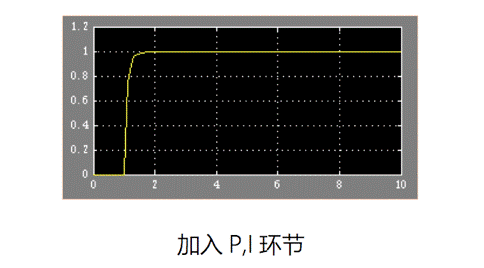
再加入 I 环节之后,稳定时纵坐标就是目标值1的位置,在I环节帮助下我们消除了稳态误差。

把示波器中的曲线想象成是步兵云台的运动,我们可以看到在加入 PID 之后,相比于前面的简单参数云台控制,现在可以实现快速而精准的枪口移动啦~
◆◆◆
由于 PID 结构简单、鲁棒性好和可靠性高等优点,是迄今为止自动控制中应用最为广泛的控制方法。从近在身边的空调温度调节,到远在太空的宇宙飞船,都离不开 PID。
在 RoboMaster 赛场上,PID 的影子也随处可见,比如说:
底盘功率控制:规则规定步兵机器人的底盘功率不能超过 80W。想让步兵机器人在 80W 限制内轻松上坡,平地上跑出最快速度,就要调好 PID。否则,一个用力过猛,爆了功率,就被判死了。

PID 没调好,爬不上坡
射频控制:规则规定步兵机器人每秒最多发射 5 个弹丸,PID 能精准地控制发射的频率,让机器人在最短时间,攻击效果最大化。

机器人连续发射
距离控制:工程机器人自动放置障碍块,PID 能精准地控制机器人与立柱的距离。

控制工程机器人与立柱的距离
控制理论一如 PID 算法的风格,是一门朴素却十分实用的理论。今天我们讲的只是管中窥豹,万物皆系统,万物皆对象,没有绝对的真理,只有正确的方法。
本期作者

电子科技大学蘑菇菌
RoboMaster 机器人代表队电控组
偶尔代码编几个游戏玩,梦想仗剑走天涯
关联专栏
RoboMaster 课程沙龙
文章标签
请问这篇文章对你有用吗?
「2019-1」【每周分享】什么是机器人比赛中的PID控制?