【分享帖】基于遗传算法的PID自整定思路介绍
56084
4
7
2021-01-25
大家好,我是好久没有登陆过RM论坛的曾经的版主花师小哲。今天来久违的更新一篇帖子。其实也是因为我这学期有门课的课程设计做了遗传算法PID自整定的相关内容,于是打算稍微写点东西。稍微搜索一下,好像没有这方面的帖子,虽然本身并不是特别复杂的算法,但有很多人对这个感兴趣,还是稍微讲一下。(熟悉的粉红大字开头)
关于PID的基本知识这里就不展开了,RM论坛里可以搜到很多资料,而且PID的思想本身也不复杂。直接正篇。
其实要用遗传算法做PID参数的自整定只需要搞懂两个问题:什么是遗传算法以及怎么样将遗传算法用过来。
先谈第一个问题,什么是遗传算法。遗传算法其实还算是一种比较常见的算法了,可以认为遗传算法是进化算法的一种,当然,这里就不谈进化算法了。
遗传算法的算法流程如下:
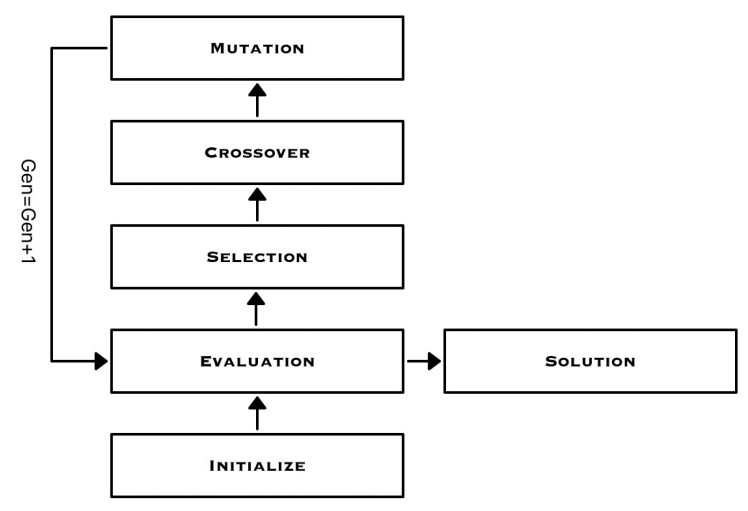
遗传算法是一种模拟生物在自然环境中的遗传、变异与进化而形成的一种自适应概率优化算法,它会根据一些启发规则逐步寻求一个最优或者近似最优的解。在达尔文的进化论中,物种进化的基本单位是种群,种群可以通过繁殖的方式将自己的部分基因传给下一代,种群中也会存在一定的变异,这就是遗传算法的思想源头。首先,我们可以生成一些初始值(这些值一般被称为个体的染色体),组成一个种群,然后我们可以让其中的一些个体进行一定的变异(染色体的值发生突变,变异也是防止种群收敛到局部最优解的一个保护措施),也可以让其中的几个个体进行“交配”(自然状态下一般是两个个体,这里其实也没那么大关系),即交换自己的部分信息。再之后,我们就可以从中选择一些“更加适应环境”的个体组成下一代的种群,这样不断迭代就可以得到一个较好的新的种群。
染色体这个词还是很形象的,因为经典的种群编码方式就是二进制编码,每个个体的值都是一串二进制,和DNA单链很像,交叉和变异也是在每个二进制位上操作的。当然,遗传算法发展到现代,其他编码方式,例如实数编码等也很常见了。
要实现遗传算法,很重要的函数就是适应度函数,这是我们进行下一代种群选择的依据,是判断一个解是否优秀的标准。
接下来就是把遗传算法应用到PID参数自整定上来了,几个点我们一一来说(以下的一些函数仅供参考,最终还是要根据实际被控对象来进行设计):
(1)怎么编码。因为我们最终的结果是三个浮点数,用二进制编码的话比较麻烦,所以个人建议用实数编码,需要注意的是,PID有三个参数,这三个参数是作为一组存在的,即每条染色体其实都是一个三元组。
(2)怎么进行交叉。需要注意的是,我们不一定要让所有个体都参与到交叉中,变异的个体就更少了。交叉的策略比较多,交叉的意义主要是交换信息,例如我们选择一种随机交换算法(p是随机值):
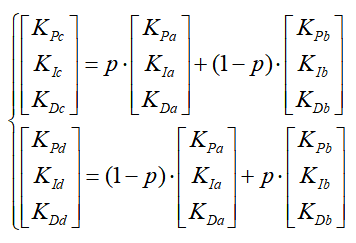
(3)怎么进行变异。实数编码下最简单的方式就是下图了(需要注意的是,PID的三个参数一般都是非负数,注意限定边界):

(4)怎么进行选择。选择也是具有随机性的,并不是说适应度高的个体就一定会留存到下一代,只是留存的概率高而已。这个还是稍微有点复杂的,例如轮盘赌算法等,这里不展开了。
(5)适应度函数如何选择。这是真正的最重要的问题,即我们要如何判断一个解是否优秀。回到PID控制本身,我们的目的是使得被控对象能够在尽量短的时间内达到我们预期的状态并且使得总体的误差(误差的绝对值的和)尽量小,更进阶的一些目标包括尽量减少超调等,这里先不考虑。
当然,一般的适应度函数都是值越大表示解更优,这也没关系,把我们之前得到的函数取个倒数就可以了,适应度函数的样子大概如下:
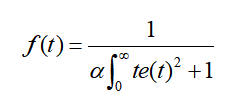
关于这些东西的选择知网能找到一大推论文的,倒不用太担心写不出好的算法。
这样其实就可以构建一个完整的系统了,当然,即使是用了遗传算法,它给出的解也只是一个近似解,最终可能还需要微调。
当然前面这些算是理论分析,虽然可以写出代码来证明其有效性,但是实际系统中还会碰到各种各样的问题。在实际控制中,被控对象往往是未知的,而计算适应度函数的过程需要每个个体都实际地控制被控对象,这会导致被控对象的状态发生改变,甚至一些很差的参数会对被控对象造成损伤。实际工程中解决这种情况的一种方法是通过定义一个初始状态,并且在每次计算适应度函数值后都尽量回到这个初始状态,并且,这样的方法还适合于遗传算法在PID控制过程中动态地调整PID参数。

蓝色是期望输出,红色是实际输出
其实做这个项目的时候,我也得到了一个已经退队的学弟的帮助,遗传算法做PID自整定是可以在实际系统中进行使用的。
关联专栏
电控开源专栏
文章标签
请问这篇文章对你有用吗?
【分享帖】基于遗传算法的PID自整定思路介绍