【分享帖】官方开源教程-系统辨识基础教程
22416
1
153
2017-10-11
上周蘑菇菌和小R给大家分享了PID控制基础教程,想必大家都看懂了吧。目前我们在调试PID的时候主要根据时域分析法,即观察时域的响应曲线调节PID参数。(听说还有小伙伴在使用经验调参和玄学调参?那你可要恶补一下了:什么是机器人比赛中的PID控制?)
使用时域分析法可以很方便的体现出系统的动态特性,例如调节时间、超调量等信息,也可以大致衡量系统的稳定性。但是如何才做到准确的判断系统的稳定性,了解系统的带宽,抑制噪声呢?这里给大家介绍一下频域分析法和系统辨识。
1. 摘要
本文介绍了对RoboMaster步兵机器人yaw轴云台速度环的系统辨识过程。引入频域分析法、传递函数、系统辨识的基本概念,介绍了J-Scope、Keil和MATLAB的fdatool和system Identification工具的应用技巧。
2. 基本概念
2.1 频域分析法
应用频率响应特性研究线性系统的经典方法称为频域分析法。
频率特性的物理意义明确,可以用分析法和实验方法获得。在进行系统分析和设计时可以应用图解法进行,直观方便。
2.2 闭环系统的传递函数
一个典型的反馈系统的结构图如图所示:
G(s)代表被控对象,C(s)为控制器,H(s)为反馈。
在不考虑扰动的情况下,系统的闭环传递函数为
因此系统可以等效为:
系统的开环传递函数为:
C(s)G(s)H(s),代表回路增益。
注意:此处的开环传递函数是针对闭环系统来说的,不是开环系统的传递函数。
由上面分析可知开环传递函数和闭环传递函数关系紧密,因此系统的开环频率特性很大程度上决定了系统的闭环性能。由于闭环系统包含反馈,校准过程较为复杂,而开环传递函数容易分析和设计,因此工程上常用开环传递函数来分析和设计控制器。
2.3 系统辨识
系统的数学模型是对该系统动态本质的一种数学描述,体现实际系统运行中的动态信息。相应的,我们也可以用实验分析方法获得表征过程动态行为的输入输出数据,建立系统的数学模型。
系统辨识得到数学模型可以用于预测系统输出的未来演变,也可以用于设计控制器来对现有系统的做出改进。
3. 基本思路
采集云台的输入输出数据(发送给yaw轴云台的目标角速度和云台的实际角速度),利用系统辨识得到传递函数,然后证明模型的正确性。
4. 实验平台和工具
硬件:RM步兵云台、stm32开发板、J-Link
软件:Keil、J-Scope、MATLAB(fdatool,systemIdentification)
5. 操作步骤
1. 在Yaw轴云台上加载速度环PID控制器,使得系统可以稳定运行
2. 写一个简单的信号发生器,将频率逐渐增加的激励信号输入至PID控制器
3. 采集并记录对应时刻的激励信号和角速度信息
4. 对输入输出数据进行系统辨识得到系统闭环传递函数,用其他方法进行验证
5.1 MPU6500滤波设置
查阅MPU6500的技术手册可知,陀螺仪有多个量程和带宽档位可以设置,为了达到更好的测量精度,需要根据应用需求进行设置。
经过初步测试,云台的正常工作角速度在±250°/s以内,因此设置量程为±250dps。
RM 6025电机能响应的电流信号频率为1kHz,根据采样定理,截止频率最高达到500Hz。因此设置MPU6500的带宽为3600Hz, 然后对数据进行低通滤波至500Hz。
如图所示,用fdatool生成截止频率为500Hz的4阶巴特沃斯滤波器:
导出系数,将传递函数形式转化为差分形式(具体过程请查阅信号与系统教材),然后在stm32工程里用C语言实现。
5.2 速度环PID控制器
根据经验和时域的响应情况,调节PID参数使得云台可以较为稳定的跟随目标角速度。
5.3 激励信号的设计
产生频率从1Hz到500Hz变化的正弦信号,每个频率点持续20个周期。由于频率范围较大,且高频部分云台振幅变化较小,为了减少数据量,采用类指数形式的变化趋势。为了保证信号不会发生跳变,在每次信号频率发生变化时都需要从零相位开始,因此周期需要是整数。使用MATLAB生成的激励信号频率如下:
F = ([1:0.5:22, 24:2:40, 50:10:120,200,250,333,500]);
T = round(1000./F); //周期取整
F = 1000./T;
5.4 数据采集和处理
编译好stm32嵌入式工程后,配置J-Scope工程,Keil进入调试模式,设置好相关参数后启动程序,用J-Scope记录云台的期望角速度和实际角速度,采集完成后导出数据为csv格式。
注意:J-Scope只能读取整型的数据,因此需要把浮点型的角速度值转化成整型(这里采用的方法是乘以1000然后转成整数)
用MATLAB导入csv文件中的数据。
由于采集到的数据前后部分存在激励信号为零的非工作状态,会影响系统辨识的结果,因此需要去除。使用find函数找到激励信号首尾第一个不为零的数据的索引值,然后根据此索引值去掉输入输出信号首尾对应的部分,得到实验所需的时域数据。
处理后的时域数据绘制如下:
5.5 系统辨识
在MATLAB的命令行窗口输入systemIdentification,打开系统辨识工具箱。
选择 Import data > Time domain data ,打开导入数据对话框,在 input 和 output 选项中键入工作区的输入输出变量名,Starting time 和 Sample time 分别输入 0 和 0.001。其他部分选填。点击 Import 将数据加入System Identification工具,然后关闭对话框。
由于本实验数据平均值为零,带宽在500Hz以内,同时需要辨识所有数据,因此无需对数据做去均值、滤波、分割等预处理。直接选择 Estimate > Transfer Function Models 打开传递函数对话框,设置零极点个数分别为1和2,点击 Estimate ,得到系统传递函数如下:
点击 Model output 和 Frequency resp 可以显示传递函数模型的拟合结果和频率响应图。
由 Model output 图像可知,该传递函数的输出结果拟合度达到88.58%,可以较好的刻画系统的动态特性。
5.6 模型验证
为了明确系统辨识得到的传递函数是否可信,可以采用以下两种方法进行验证。
5.6.1 直接测量不同频率下的幅度比和相位差
在stm32的程序中,通过查找一定时间内的云台角速度的极值找出幅度,通过计算输入输出信号上升沿穿过x轴的时间差除以周期来计算该频率下的相位差。
将不同频率点的幅度和相位数据保存在数组中,用Keil的SAVE命令导出内存数据(hex格式),经过处理(删除标志信息、数据分段、16进制转浮点数)后得到实测的频域数据,绘制bode图如下
5.6.2 FFT处理时域数据
对时域数据做fft变换,然后计算输入输出数据的幅度比和相位差,得到系统的频率响应:
5.6.3 综合对比
对比三种方式得到的频率响应曲线:
由图可见,在低频部分,系统辨识得到的传递函数能够较好的拟合fft变换的结果和实测的频率响应结果,因此可以用该传递函数来刻画yaw轴云台系统。
由bode图可以看出3dB带宽大概为40rad/s,实际意义就是该云台系统能够响应的频率6.4Hz以内。
参考资料:
1. J-Scope介绍及资料下载:https://www.segger.com/products/debug-probes/j-link/tools/j-scope
2. System Identification 官方帮助文档:https://cn.mathworks.com/help/ident/index.html
3. Keil的SAVE命令用法:http://www.keil.com/support/man/docs/uv4/uv4_cm_save.htm
https://wenku.baidu.com/view/f5edb390551810a6f424865b.html
4. 奥本海姆. 《信号与系统(第二版)》. 电子工业出版社
5. 胡寿松. 《自动控制原理(第四版)》. 科学出版社
6. 萧德云.《系统辨识理论及应用》.清华大学出版社
得到系统闭环传递函数后,经过处理可以得到开环传递函数进一步分析系统稳定性,还可以用频率分析法对环路进行整形,从而达到我们想要的性能,具体操作步骤会在后续的文章给大家介绍。敬请期待!
最后,欢迎大家跟帖提出问题和建议。
使用时域分析法可以很方便的体现出系统的动态特性,例如调节时间、超调量等信息,也可以大致衡量系统的稳定性。但是如何才做到准确的判断系统的稳定性,了解系统的带宽,抑制噪声呢?这里给大家介绍一下频域分析法和系统辨识。
1. 摘要
本文介绍了对RoboMaster步兵机器人yaw轴云台速度环的系统辨识过程。引入频域分析法、传递函数、系统辨识的基本概念,介绍了J-Scope、Keil和MATLAB的fdatool和system Identification工具的应用技巧。
2. 基本概念
2.1 频域分析法
应用频率响应特性研究线性系统的经典方法称为频域分析法。
频率特性的物理意义明确,可以用分析法和实验方法获得。在进行系统分析和设计时可以应用图解法进行,直观方便。
2.2 闭环系统的传递函数
一个典型的反馈系统的结构图如图所示:
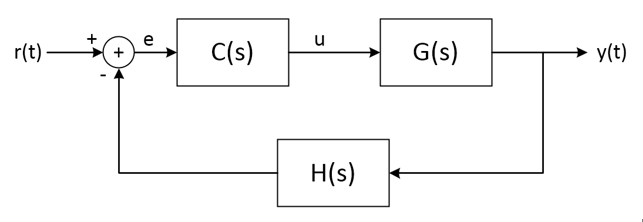
G(s)代表被控对象,C(s)为控制器,H(s)为反馈。
在不考虑扰动的情况下,系统的闭环传递函数为
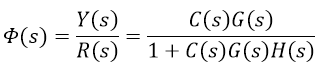
因此系统可以等效为:
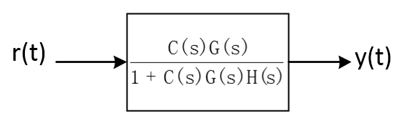
系统的开环传递函数为:
C(s)G(s)H(s),代表回路增益。
注意:此处的开环传递函数是针对闭环系统来说的,不是开环系统的传递函数。
由上面分析可知开环传递函数和闭环传递函数关系紧密,因此系统的开环频率特性很大程度上决定了系统的闭环性能。由于闭环系统包含反馈,校准过程较为复杂,而开环传递函数容易分析和设计,因此工程上常用开环传递函数来分析和设计控制器。
2.3 系统辨识
系统的数学模型是对该系统动态本质的一种数学描述,体现实际系统运行中的动态信息。相应的,我们也可以用实验分析方法获得表征过程动态行为的输入输出数据,建立系统的数学模型。
系统辨识得到数学模型可以用于预测系统输出的未来演变,也可以用于设计控制器来对现有系统的做出改进。
3. 基本思路
采集云台的输入输出数据(发送给yaw轴云台的目标角速度和云台的实际角速度),利用系统辨识得到传递函数,然后证明模型的正确性。
4. 实验平台和工具
硬件:RM步兵云台、stm32开发板、J-Link
软件:Keil、J-Scope、MATLAB(fdatool,systemIdentification)
5. 操作步骤
1. 在Yaw轴云台上加载速度环PID控制器,使得系统可以稳定运行
2. 写一个简单的信号发生器,将频率逐渐增加的激励信号输入至PID控制器
3. 采集并记录对应时刻的激励信号和角速度信息
4. 对输入输出数据进行系统辨识得到系统闭环传递函数,用其他方法进行验证
5.1 MPU6500滤波设置
查阅MPU6500的技术手册可知,陀螺仪有多个量程和带宽档位可以设置,为了达到更好的测量精度,需要根据应用需求进行设置。
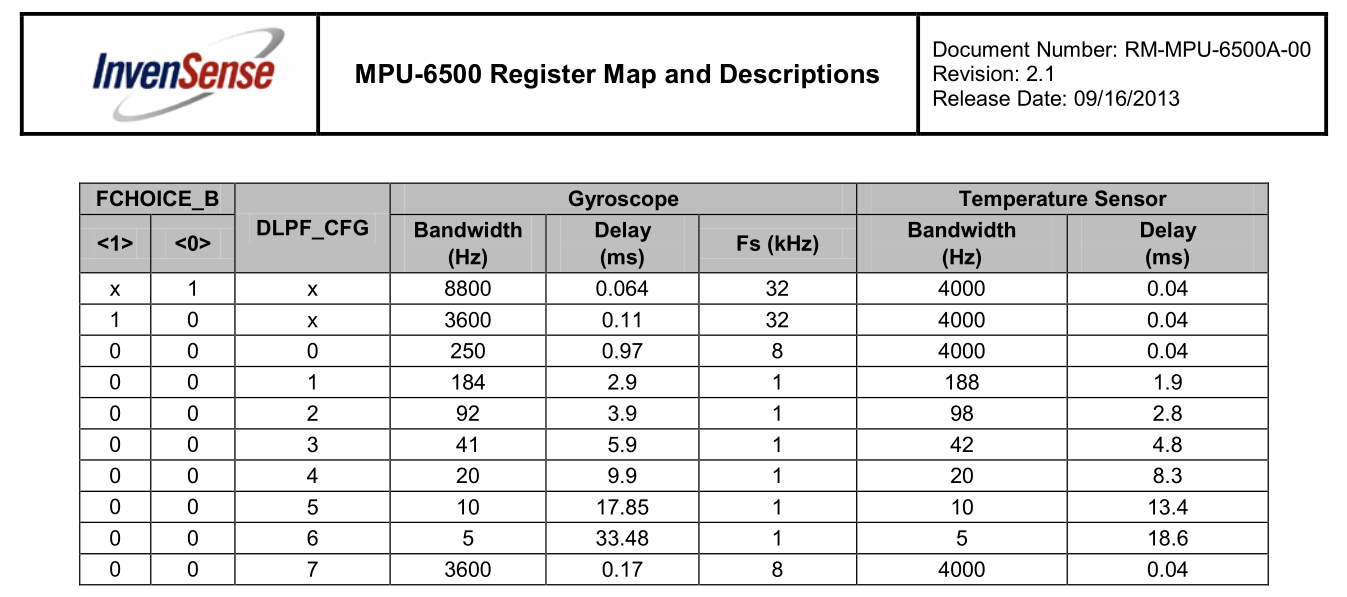

经过初步测试,云台的正常工作角速度在±250°/s以内,因此设置量程为±250dps。
RM 6025电机能响应的电流信号频率为1kHz,根据采样定理,截止频率最高达到500Hz。因此设置MPU6500的带宽为3600Hz, 然后对数据进行低通滤波至500Hz。
如图所示,用fdatool生成截止频率为500Hz的4阶巴特沃斯滤波器:
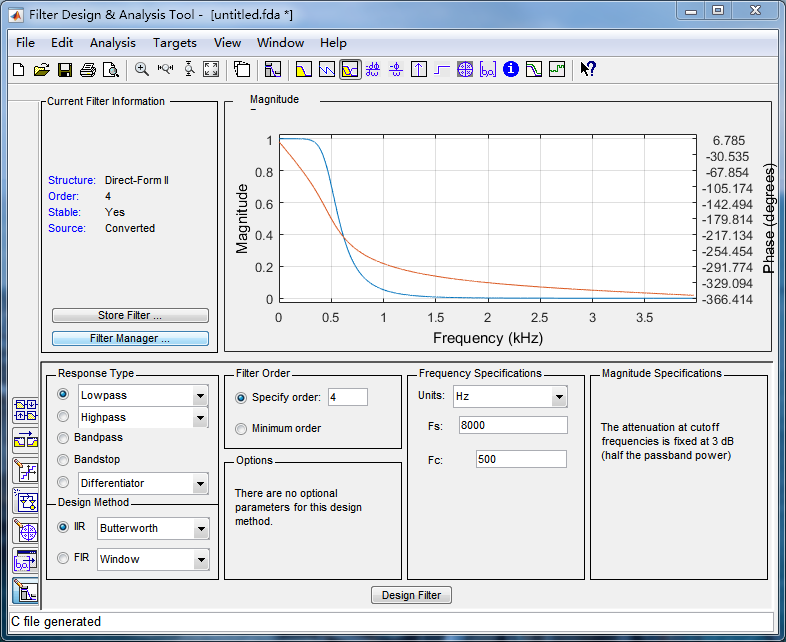
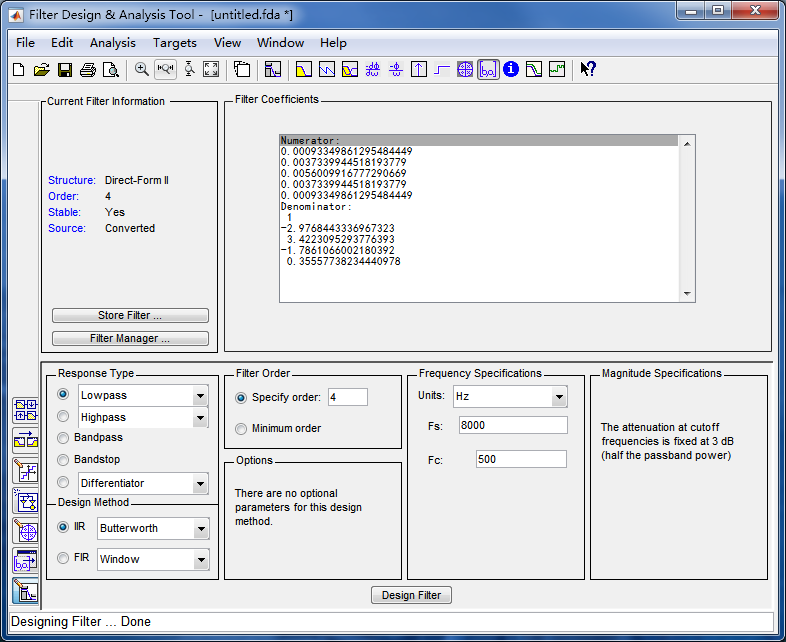
导出系数,将传递函数形式转化为差分形式(具体过程请查阅信号与系统教材),然后在stm32工程里用C语言实现。
5.2 速度环PID控制器
根据经验和时域的响应情况,调节PID参数使得云台可以较为稳定的跟随目标角速度。
5.3 激励信号的设计
产生频率从1Hz到500Hz变化的正弦信号,每个频率点持续20个周期。由于频率范围较大,且高频部分云台振幅变化较小,为了减少数据量,采用类指数形式的变化趋势。为了保证信号不会发生跳变,在每次信号频率发生变化时都需要从零相位开始,因此周期需要是整数。使用MATLAB生成的激励信号频率如下:
F = ([1:0.5:22, 24:2:40, 50:10:120,200,250,333,500]);
T = round(1000./F); //周期取整
F = 1000./T;
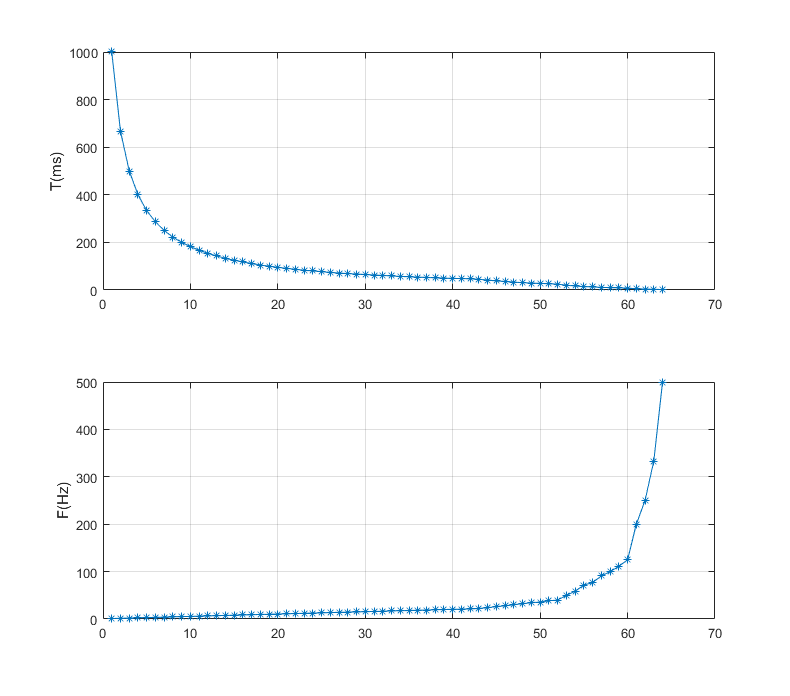
5.4 数据采集和处理
编译好stm32嵌入式工程后,配置J-Scope工程,Keil进入调试模式,设置好相关参数后启动程序,用J-Scope记录云台的期望角速度和实际角速度,采集完成后导出数据为csv格式。
注意:J-Scope只能读取整型的数据,因此需要把浮点型的角速度值转化成整型(这里采用的方法是乘以1000然后转成整数)
用MATLAB导入csv文件中的数据。
由于采集到的数据前后部分存在激励信号为零的非工作状态,会影响系统辨识的结果,因此需要去除。使用find函数找到激励信号首尾第一个不为零的数据的索引值,然后根据此索引值去掉输入输出信号首尾对应的部分,得到实验所需的时域数据。
处理后的时域数据绘制如下:
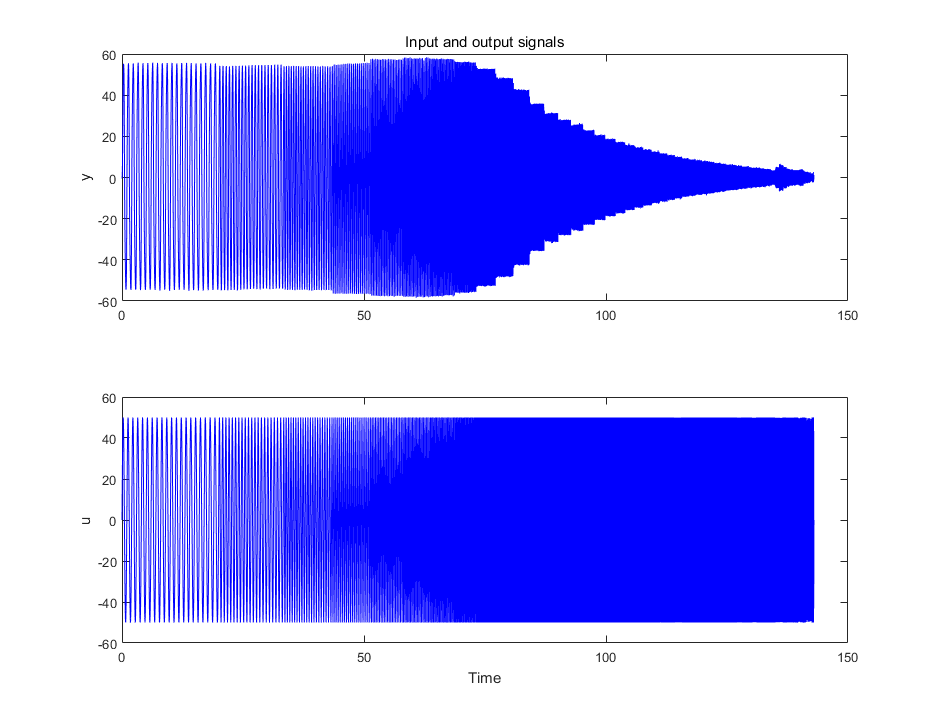
5.5 系统辨识
在MATLAB的命令行窗口输入systemIdentification,打开系统辨识工具箱。
选择 Import data > Time domain data ,打开导入数据对话框,在 input 和 output 选项中键入工作区的输入输出变量名,Starting time 和 Sample time 分别输入 0 和 0.001。其他部分选填。点击 Import 将数据加入System Identification工具,然后关闭对话框。
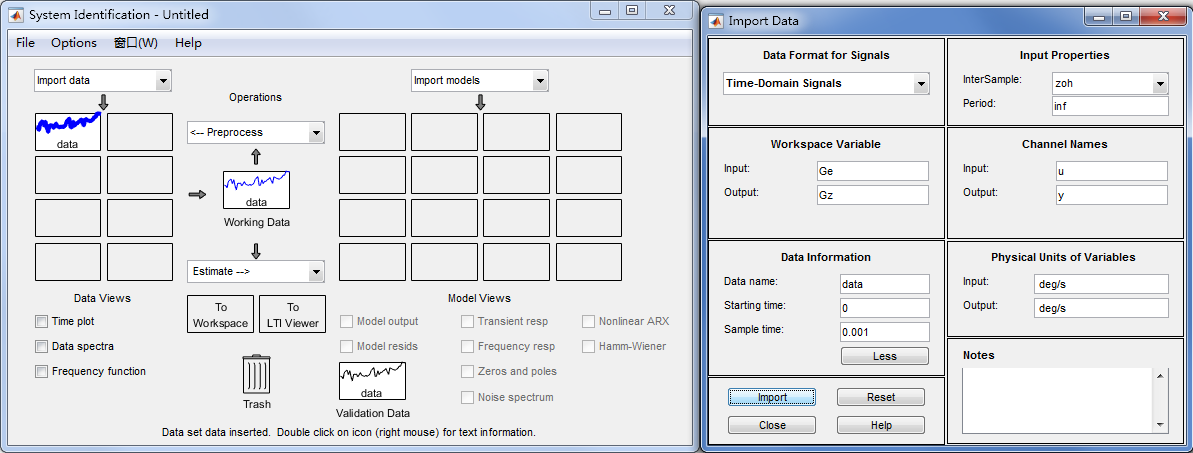
由于本实验数据平均值为零,带宽在500Hz以内,同时需要辨识所有数据,因此无需对数据做去均值、滤波、分割等预处理。直接选择 Estimate > Transfer Function Models 打开传递函数对话框,设置零极点个数分别为1和2,点击 Estimate ,得到系统传递函数如下:
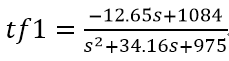
点击 Model output 和 Frequency resp 可以显示传递函数模型的拟合结果和频率响应图。
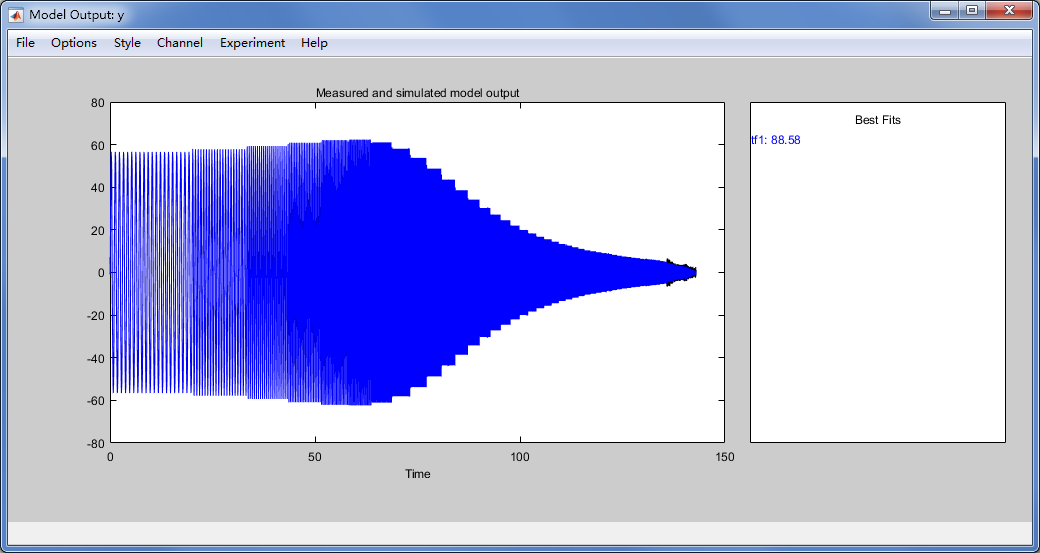
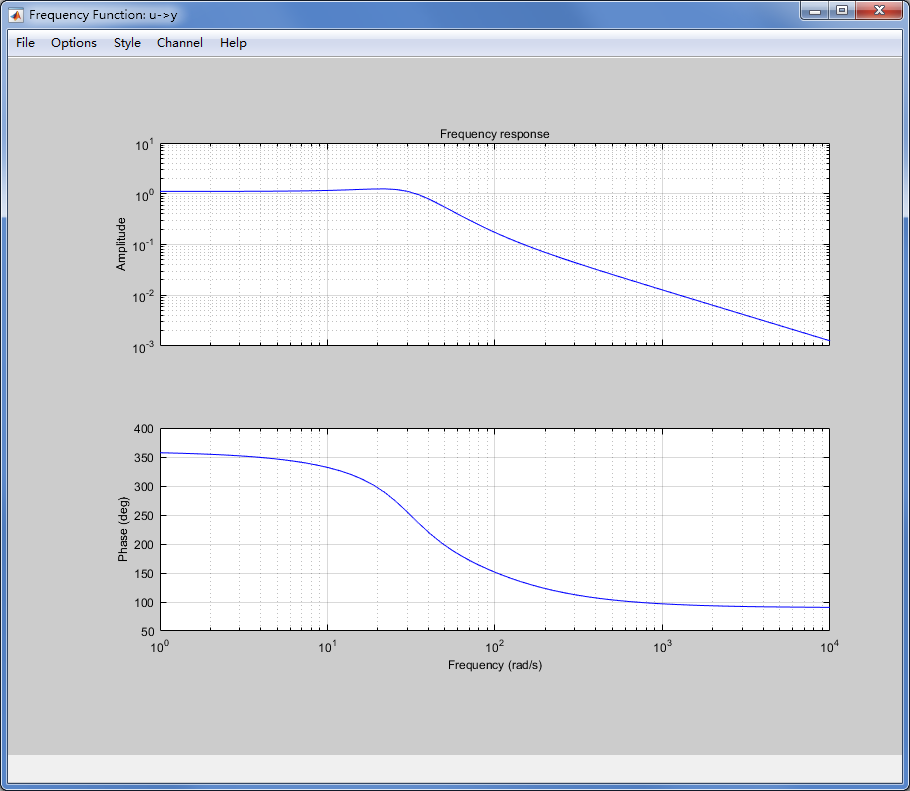
由 Model output 图像可知,该传递函数的输出结果拟合度达到88.58%,可以较好的刻画系统的动态特性。
5.6 模型验证
为了明确系统辨识得到的传递函数是否可信,可以采用以下两种方法进行验证。
5.6.1 直接测量不同频率下的幅度比和相位差
在stm32的程序中,通过查找一定时间内的云台角速度的极值找出幅度,通过计算输入输出信号上升沿穿过x轴的时间差除以周期来计算该频率下的相位差。
将不同频率点的幅度和相位数据保存在数组中,用Keil的SAVE命令导出内存数据(hex格式),经过处理(删除标志信息、数据分段、16进制转浮点数)后得到实测的频域数据,绘制bode图如下
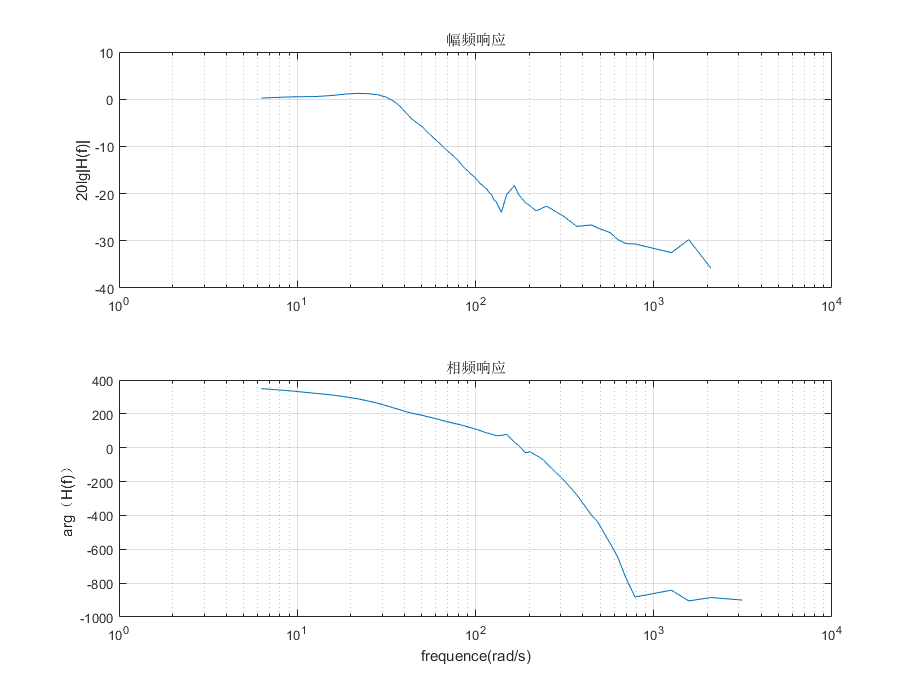
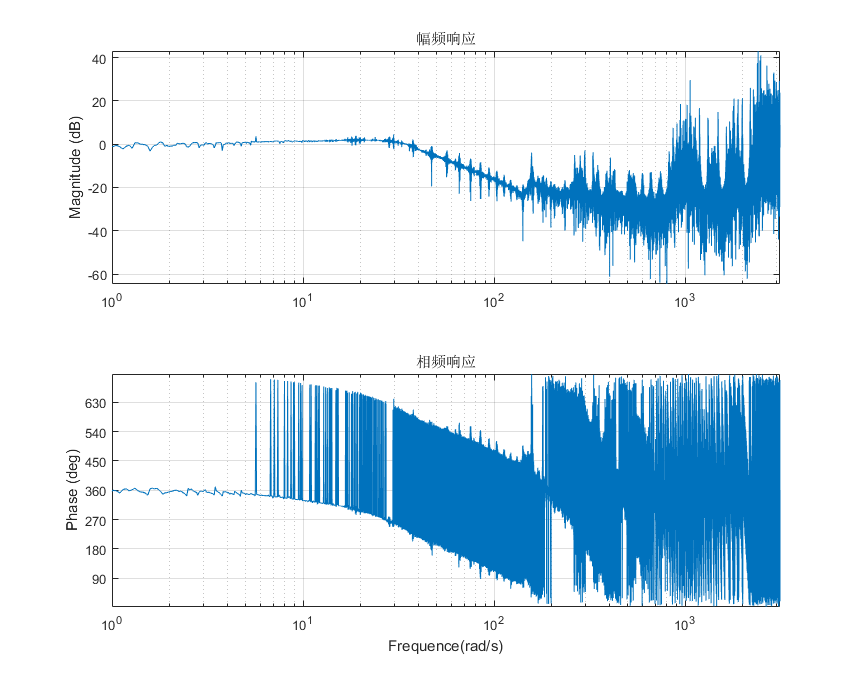
5.6.2 FFT处理时域数据
对时域数据做fft变换,然后计算输入输出数据的幅度比和相位差,得到系统的频率响应:
5.6.3 综合对比
对比三种方式得到的频率响应曲线:
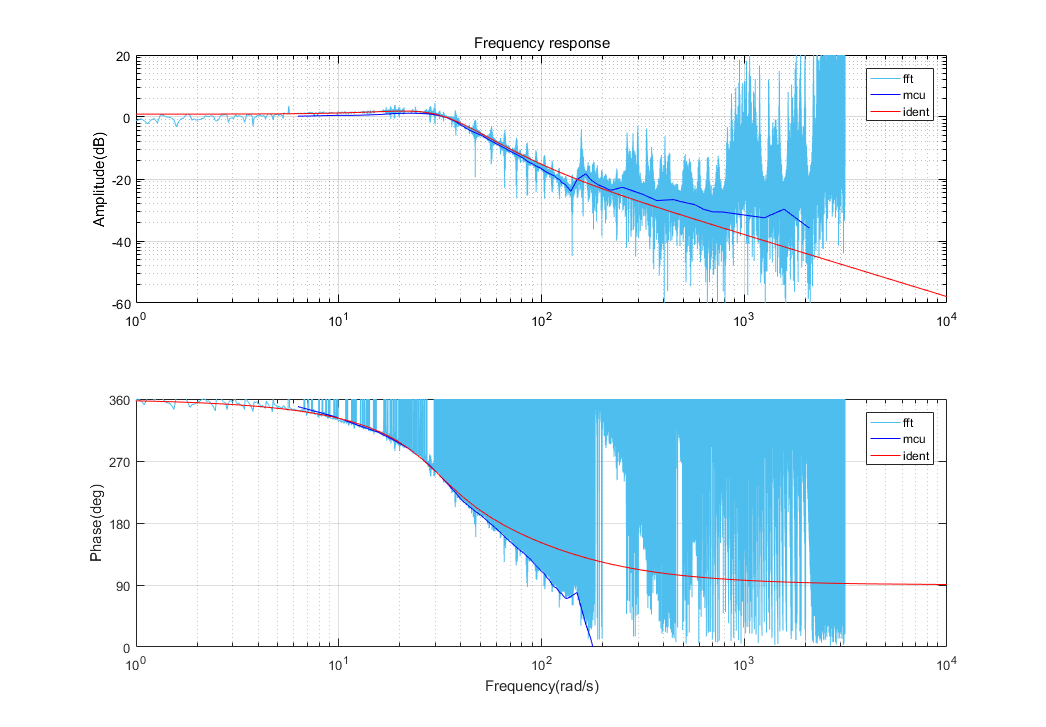
由图可见,在低频部分,系统辨识得到的传递函数能够较好的拟合fft变换的结果和实测的频率响应结果,因此可以用该传递函数来刻画yaw轴云台系统。
由bode图可以看出3dB带宽大概为40rad/s,实际意义就是该云台系统能够响应的频率6.4Hz以内。
参考资料:
1. J-Scope介绍及资料下载:https://www.segger.com/products/debug-probes/j-link/tools/j-scope
2. System Identification 官方帮助文档:https://cn.mathworks.com/help/ident/index.html
3. Keil的SAVE命令用法:http://www.keil.com/support/man/docs/uv4/uv4_cm_save.htm
https://wenku.baidu.com/view/f5edb390551810a6f424865b.html
4. 奥本海姆. 《信号与系统(第二版)》. 电子工业出版社
5. 胡寿松. 《自动控制原理(第四版)》. 科学出版社
6. 萧德云.《系统辨识理论及应用》.清华大学出版社
得到系统闭环传递函数后,经过处理可以得到开环传递函数进一步分析系统稳定性,还可以用频率分析法对环路进行整形,从而达到我们想要的性能,具体操作步骤会在后续的文章给大家介绍。敬请期待!
最后,欢迎大家跟帖提出问题和建议。
关联专栏
电控开源专栏
算法开源专栏
文章标签
请问这篇文章对你有用吗?
【分享帖】官方开源教程-系统辨识基础教程