【分享帖】第七课时 控制技术 PID控制中的I与D(一)
12965
0
10
2018-03-29
PID控制算法是《RoboMaster机器人基础》中最难的一个知识点,但是它对于机器人的控制来说却尤为重要。PID算法是机器人控制方面应用最广泛的算法,理解PID控制原理将在今后帮助大家更好地控制机器人。
这篇文章首先会为大家准备一个学习PID的“知识工具箱”。这个工具箱里包括了数学词汇,符号,和其他数学工具。
先让我们学习和回顾一些相关的数学概念。
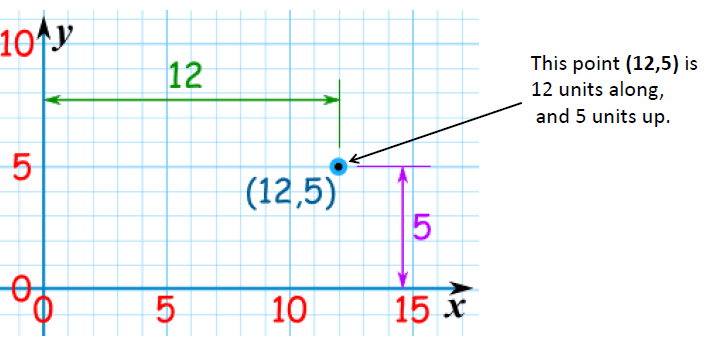
1. 点(Point)
一个点是一个确切的位置。它没有大小或是维度。
2. 无穷(Infinity)
“无穷”是指一个东西没有尽头,没有边界,无穷无尽。我们用“∞”这个符号来表示“无穷”。
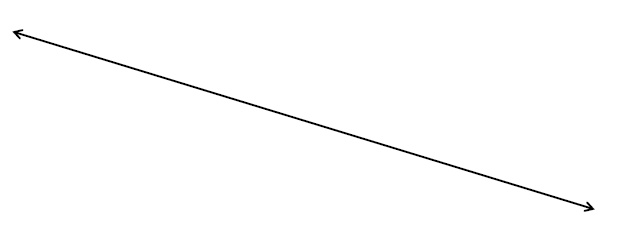
3. 线(line)
一条线只有一个维度,它由无数个点相连组成。
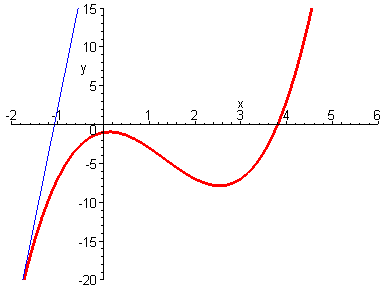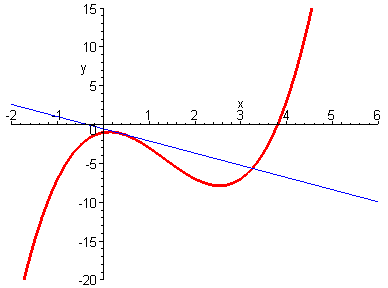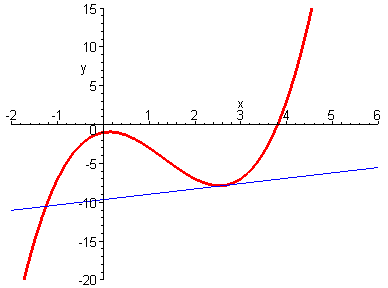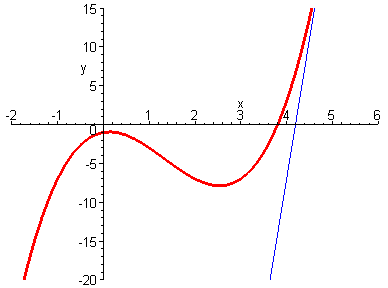
4. 切线(tangent line)
切线指的是一条刚好触碰到曲线上某一点的直线,更准确地说,当切线经过曲线上的某点(即切点)时,切线的方向与曲线上该点的方向是相同的。
5. 变量(variable)
变量可以是一个符号,一个字母,一个单词去包含一个数值(如一个整数,一个实数)。下面公式中的x就是一个变量。

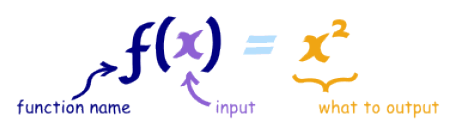
6. 函数(function)
一个函数将输入和输出以某种特殊关系联系起来。换句话说,一个函数再接受到输入以后,对输入的数据进行处理然后产生一个输出。在下面的一个函数里,f()是函数名,x是该函数的输入,x的平方是该函数的输出
7. Delta (符号:Δ)
Δ表示数值之间的变化量。
举例:如果一个光传感器在采样时数值从75变成了50,我们说Delta为-25或是Δ=-25(50-75 = -25)。
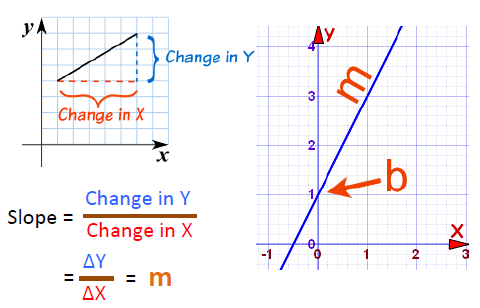
8. 斜率(Slope/Gradient)
一条直线的斜率可以通过以下方式表示:
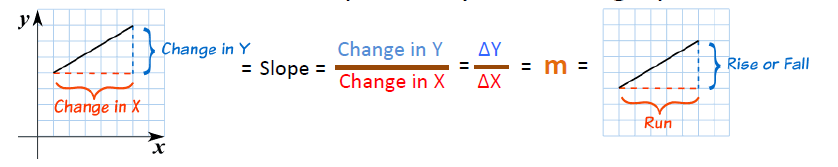
从上图中x,y的坐标系中可以看到如果我们将一个点从左下方移动到右上方,那么在x方向上的变化量为图中的“change in X”(ΔX),y方向的变化量为“change in Y”(ΔY),它们之间的比值“m”就是这条线的斜率。
下图是三个求直线斜率的例子,从左到右三根线的斜率分别为2,-2和0。

9. 求和(Summation)(符号:Σ)
Σ代表将所有的数值相加求和。
举个例子 ,1到9的Σ为“1+2+3+4+5+6+7+8+9=45”。
10. 直线的表达式
我们可以用变量来描述图中的任何直线,如下图中的直线可以被表示为 y=mx+b
11. 微分
从书中我们已经知道PID中的三个大写英文字母分别对应的是P(Proportional 比例),I (Integral 积分)和D(Derivative 微分)。我们先通过一种通俗易懂的方式来学一学微分也就是PID中的D。

假设Jack 和 Jill两个小朋友要爬上一个小山丘去打水,我们将它们的运动位置拆分成水平距离(Distance)和高度(Height)。在山丘上的他们任意的一个位置都可以通过“距离”+ “高度”来进行表示。
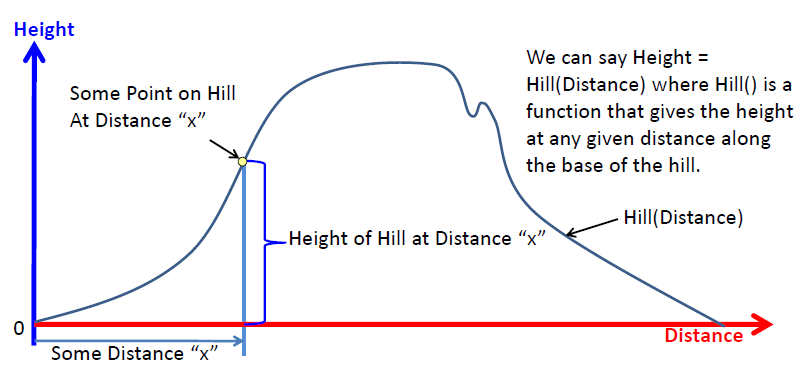
从上图中的小黄点可以看到,当行走的水平距离为x的时候,这个水平距离x会对应沙丘上的一个高度。因此,我们可以说山丘的“高度(Height)”是关于“距离(Distance)”的一个函数,该函数可以表达为 Height = Hill(Distance) , 其中Hill()是函数的名字,对于任何Distance的输入,都可以通过这个函数来输出一个相对应的高度(Height)。
更多关于微分和PID相关的其他内容请见下一篇文章 PID控制中的基本概念(二)。
文章标签
请问这篇文章对你有用吗?
【分享帖】第七课时 控制技术 PID控制中的I与D(一)