【分享帖】第七课时 控制技术 PID中的I与D(三)
7961
0
9
2018-03-30
接着上篇文章我们继续讨论,本篇文章主要讲解关于导函数,和积分的一些基础知识。
导函数:
导函数是一个表述函数上每个点斜率的函数,任何一个函数都会有对应的导函数,如上篇文章里的HillSlope()函数就是Hill()函数的导函数。利用在上篇文章里提到的用穿过两个相邻点的直线来估算斜率的方式(如下图所示),我们可以将一个导函数写成这种形式:
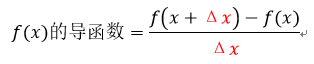
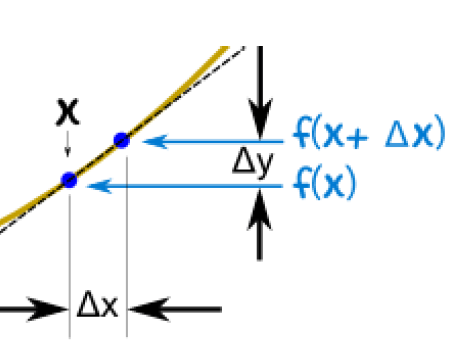
积分(Integral):
积分是微分的逆运算,我们可以对一个函数进行积分来求得它的积分函数。
如下图中的例子,下面图中的第一幅图描述的是自行车速度随时间变化的图像,从图像中可以看出,自行车一共行驶了5个小时,在第1个小时内自行车速度为5miles/hour, 在第2和第3个小时内,自行车的速度为10miles/hour, 第4个小时内的速度为15miles/hour,第5个小时内的速度为5miles/hr。如果我们想要知道在这5个小时内自行车行驶的总距离,最简单的计算方法就是将每段时间内行驶过的距离相累加起来。
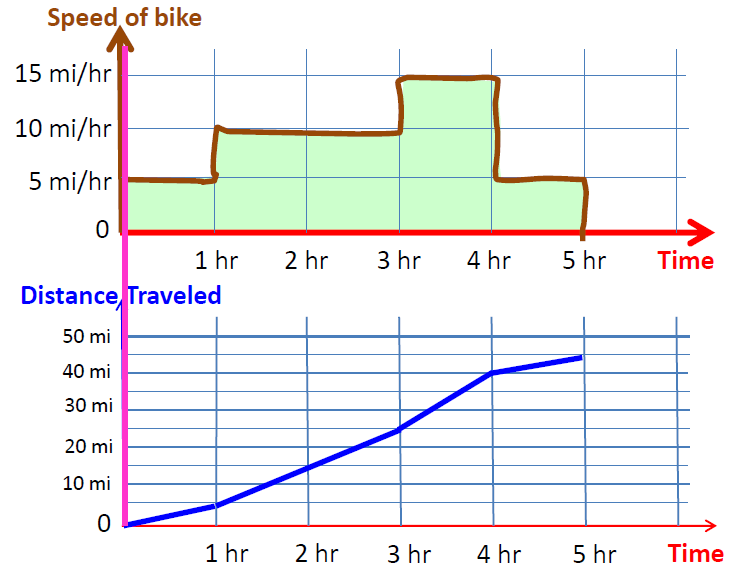
我们通过将每段时间内的速度与时间相乘来计算总距离:
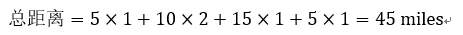
所以5小时内自行车行驶过的总距离是45miles。
现在我们将上述累加距离的过程在一张新的坐标图中用一个一个点标出,并用直线将这些点两两相连,这样就可以得到第二幅图,这幅图展现的就是自行车行驶距离叠加的过程。可以看到,第二幅图尾端所对应的数值为45miles。
实际上,上面的将每一小段时间内行驶过的距离累加起来的过程就是积分的一个过程。其实我们可以换一种角度来看,求积分的过程也可以理解为求函数下方面积的过程,在这个例子中,上图中被涂成绿色的面积就等于自行车行驶过的总过程。从上述自行车的例子中可以看出,积分的过程实际上就是找出函数下方面积的过程,举个例子,假设我们现在要对下图中的函数f(x)进行积分,那么积分后的表达式应该被写为:
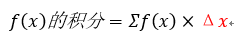
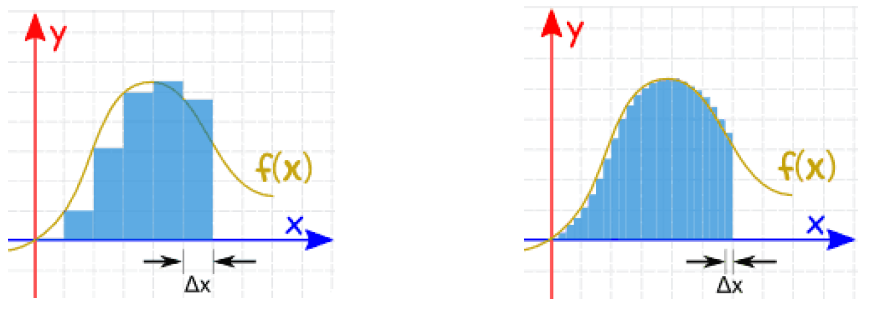
我们可以通过下面两幅图来理解一下这个积分的表达式:从下图中可以看到,对于每一个小长方形我们用长乘宽的方式将它们各自的面积求出,这些小长方形的宽,长为每一个横坐标在函数f(x)上对应的值。从左图中可以看到,如果我们将这些小长方形的面积叠加就可以粗略得估算出函数下的面积,如果我们设置得非常小(如右图),那我们就可以较为精准地求出函数下的面积,也就是函数的积分值。
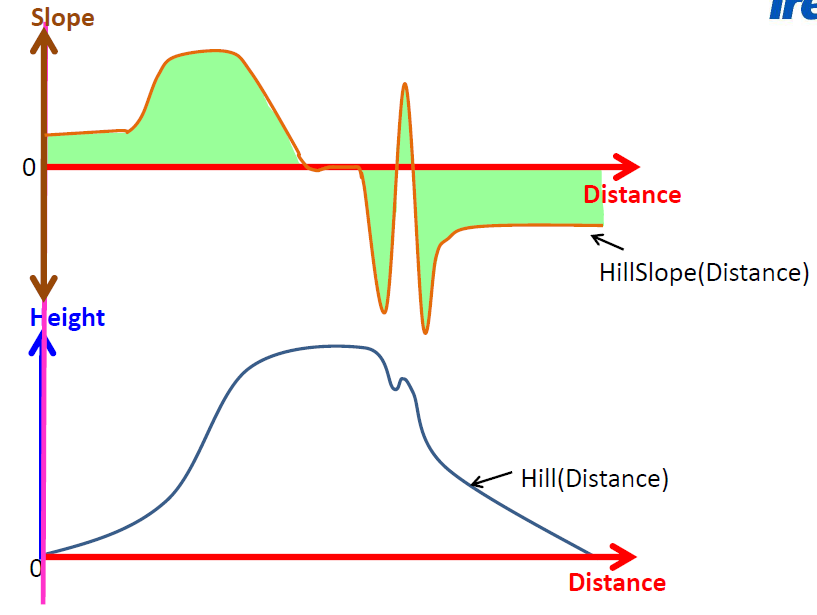
再让我们回顾一下Jack 和Jill的例子,这里大家可以回想一下之前的Hill()函数的导函数HillSlope()么,如果我们现在想求它的积分函数,我们只要将HillSlope()下的面积叠加起来便可以得到最原始的Hill()函数。这也验证了我们之前说的积分是微分的逆运算这一说法。
文章标签
请问这篇文章对你有用吗?
【分享帖】第七课时 控制技术 PID中的I与D(三)